I feel like I’ve been preaching the gospel of vertical non-permanent surfaces and visible random groups everywhere I go these days. The norm is set in my room – I pose the problem, give them a couple minutes of silent thought, put them in groups, and away they go.
Below is a pattern I made up quickly one morning. It doesn’t look exciting – but guess what? It’s doesn’t have to be. It was close enough to full class engagement for me, which was due to a nice combination of:
1. They believed they could do it.
2. Vertical non-permanent surfaces and visible random groupings.
3. Probably some other things I can’t quite pin down yet.
I’ve settled on these as my go-to questions for visual patterns. I know I got the sketch the 10th idea from Fawn’s blog. I never used to have them do that but when I started requiring it I was impressed with how helpful it was for a lot of my students when they ultimately wrote the equation.
1. Sketch the 10th
(helps them immensely when writing the equation)
(sketches aren’t exact drawings. I tell them I should be able to have them sketch the 1,000,000th)
2. How many blocks are in the 49th?
(too big for a table! For students struggling to write an equation, having them sketch the 49th usually gets them to get it)
3. How many blocks are in the nth?
(I start the year asking it this way: “Write an equation that relates the step number to the number of blocks in that step. (another way to ask this question is: How many blocks are in the nth step?)”
I would literally have that parenthesis in each problem, until I finally got to drop it.)
4. What is the largest step I could build with 1000 blocks?
The first extension. My true goal here is the equation in #3.
5. How much of the sequence could I build with 1000 blocks?
A second extension. It’s quadratic and I haven’t directly covered quadratics, so it will challenge those kids. We have talked about Gauss addition so it is not completely out of their range.
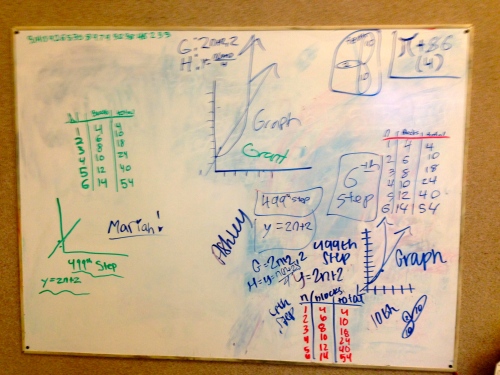
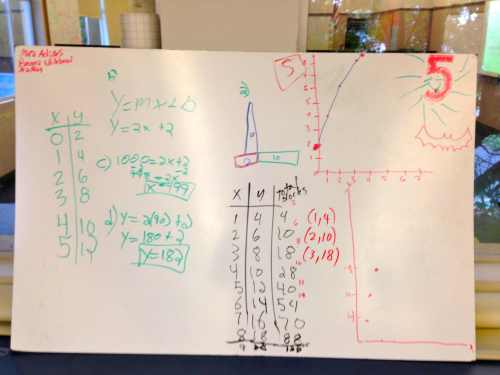
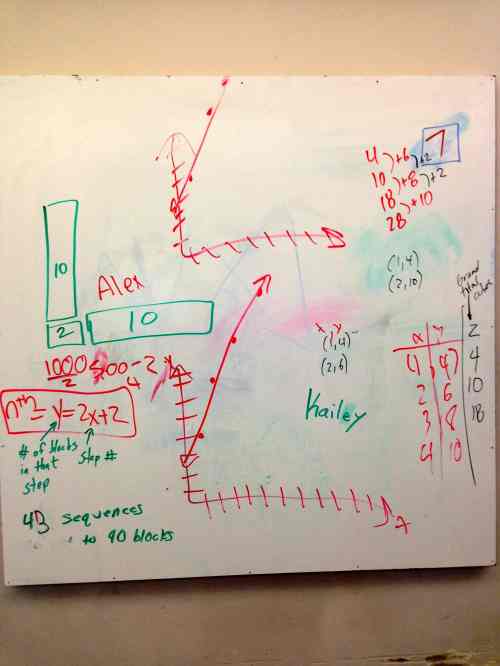
On the whiteboards below you will see graphs because in this particular case I also asked them to graph the number of blocks per step, and the total number of blocks needed to build the entire sequence per step. I wanted them to have to graph something non-linear. I think it helps further highlight what makes things linear when they work with things that aren’t.
They don’t go directly to the whiteboards. I first give them about 5 minutes to develop their own thoughts in quiet. Then I group them and they do their thing.
After class I always look at every whiteboard and judge how much of the conclusions are in their writing vs my writing. I’m not sure what I gain from that but it is a research point for me right now. There is a little bit of my writing on boards 7 and 5, but they are supplementary thoughts and not the main thinking that I wanted to the students to do. Here are some of the whiteboards after the activity:
Lastly, after it was finished I had them go back to that paper with their initial thoughts and complete the problem on paper. I give them graph paper and rulers and have them make nice graphs to turn into me. In some sense, one could think of the paper as the assignment as the whiteboard as a giant scaffolding. But in another sense the whiteboards could be the assignment, and the paper is something that goes in the notes. Or in another sense…