My First Class

I remember the very first time I stood up in front of a room of teenagers and asked them to do something.  I nervously gave them a scattered lecture on the intricacies of y = mx + b.  As I was talking they were writing down the things I was saying, and whatever I put on the whiteboard they also put into their notebook.  During the lecture I even asked the students some questions, and a few of them even raised their hands and offer up answers.  Next I told them to get out their workbooks and there was a huge rustling of paper as they actually did it.  I told them to go to section 5-4 and do problems #1 – 20 or something like that, don’t remember the exact numbers.  Either way, in unison the class asked me “which page number is that?”, I mean it was probably only two students but it felt like they were all asking.  I learned students prefer page numbers to section numbers.

At that point it was about answering individual questions.  So I basically just floated up and down the rows, or at least it seemed like I floated because I don’t remember hearing my footsteps.  Or maybe I just ignored them because the sounds in the room were really beautiful – I was hearing words I wasn’t used to hearing teenagers say, like “slope” and “intercept”.  And I was hearing words more familiar to me like “yesterday” and “that’s cool”.  The students all knew each other because it was the middle of the year.  I was just there for one day as a requirement before beginning a student teaching assignment.  I was a guest in their house.

At the end of the period they all turned in their papers to me – full of calculations and circled answers.  And their names were all at the top right even though I never asked them to do that.  Then a bell sounded and they all packed up and left.  I looked at their papers, more specifically their names, and thought about how cool it would be if I actually knew who they were.  If I was actually their teacher.

I was amazed at the whole experience.  And I’m not saying it was the ideal class, nor am I advocating for any particular teaching strategy – I’m just saying I was amazed.

Missing Assignment Buyout Program

The Overview:

This year I wanted to do Kyle Pearce’s Detention Buyout Program that Dan had highlighted in his Great Classroom Action series.  The problem was that in my new school we don’t have detentions, so I didn’t think I would get much buy-in from the students.  But there is something that all schools definitely do have:  Missing assignments!  So I created three “deals” that would allow students to pay me money in exchange for getting credit for an assignment they missed.

I used this assignment as an introduction to inequalities, but I also wanted to link the Missing Assignment Buyout Program to the linear equations we just finished covering.  That is the why as you look at this assignment, you will see a focus on connecting the information in the graphs to the information contained in the inequalities.

I sequenced this by first giving the assignment.  Then two days later I did another version of it as an opener / warmup.  And then lastly I put another version of it on their test.  Each new version offered slight modifications from the previous.

The Description:

I first offer students three possible deals for buying off their missing assignments.  I poker face the whole thing and enjoy all the “Is this legal” expressions on their faces.  I tell them to make sure they go home and talk to their parents about how much money they have budgeted for such as program.  The first question on the worksheet asks them which deal is better for them, so as an added bonus I printed out each students missing assignments and handed it to them.  This is that first worksheet:

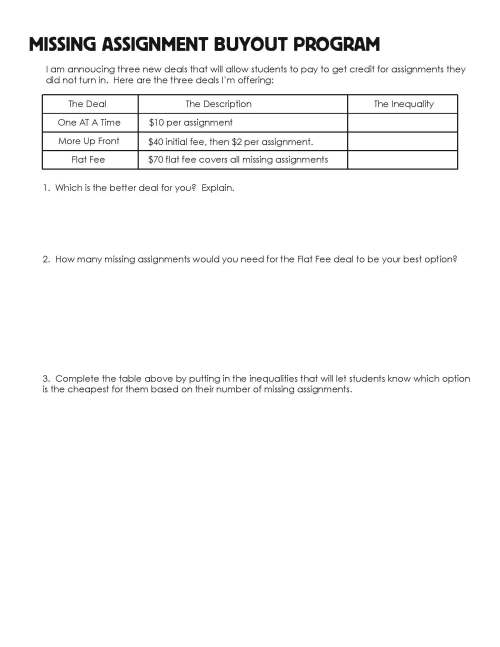
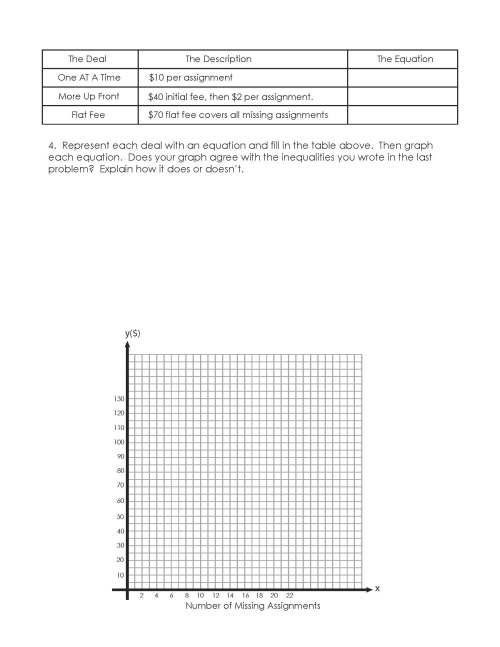
There are a lot of interesting questions and explanations that came out of this first assignment.  For instance, having students see that x less than 5 was the same as saying x less than or equal to 4 since x could only take integer values.  Also having students see the connection between the intersection points of their graphs and the inequalities they wrote was time well spent.

A couple days later I came back to the Missing Assignment Buyout Program in the form of a opener or warmup question.  I handed the students this graph when they came into the room (two graphs per page to save paper):

Then I had students write a description of each deal, as well as the inequality and equation for each deal.  This was a slight inversion of the original assignment where I gave them the description and had them write the inequality, equation, and then graph.  Now I am giving them the graph and asking them to write the description, inequality, equation.  I have them in pairs and am checking homework and taking role while they work.  Then I randomly call on pair share partners and fill in the following table that I am projecting on the board:

Lastly to make sure that they really did understand the concept, I put a similar problem to the opener exercise in their inequalities chapter test.  The test had a slight twist in a scenario where a student would want to buy the Flat Fee plan based on their number of missing assignments, but based on the money they had to spend, they would need to pick their second best option.  Here’s that problem:

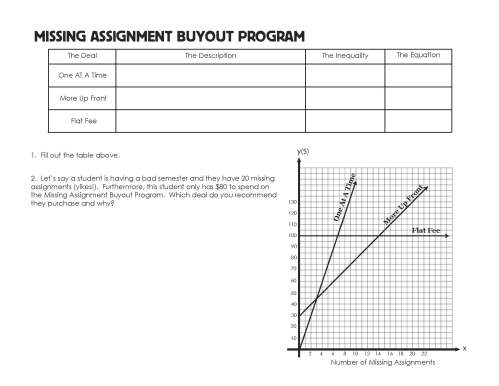
I initially thought having them graph each deal was kind of an unnatural excercise, because why would someone ever graph something like that?  But I think it ended up working because of how the Opener and Test question both refer to the graph.  All in all student engagement was high, even with the graphing portion so I think I’ll keep it next year.

The Extension:

(good idea courtesy of my principal)

Tell the students that you have decided to only offer one deal to the whole class, and they have to decide which deal they want for the class.  This could open up a nice debate about fairness and equity – this deal is best for you since you don’t have any missing assignments, but what about these other students?  Connect this debate to something current, like Obamacare.  Discuss how math influences decisions and that often decision makers have to make decisions based on their believe on the greater good, even when the numbers indicate that some people will be negatively affected by the decision.

The Goods:

MissingAssignmentBuyoutProgram

MissingAssignmentBuybackProgramOpener

MissingAssignmentBuybackProgramTest

My Fellow Teacher

“How’s it going my fellow teacher?”  One of my students told me that.

I’ve been telling my students that people call me a teacher because I get paid to teach. But being a teacher isn’t about a paycheck – it’s about teaching someone something. So all my students are teachers because of all the times they work together and help each other. When we pair share I will say things like “give your fellow teacher a fist bump before we get started”, and they will give each other a fist bump. It has been fun to watch them pick up and run with the message.

Motivation 101 – Define Success

I tell students that success in our class means everyday you leave better than you showed up.  And to leave better means you learned at least one thing about algebra.  It doesn’t matter if you have an A or an F, that simply measures how you have done in the past – but today you are success if you can learn one thing.

Everyday I write the goal for the days lesson on the board.  The goal could be to simplify rational expressions, but I always remind the students that the actual goal is to learn at least one thing about algebra.

I tell students to look for things they don’t understand and be excited when they encounter them because it is precisely those things that are going to make them a success.   If I’m helping a student and they get it – they go from a place or not knowing to knowing, I tell them “good job, you’re a success today, keep it up”.

At the end of class I always recap the day for the final couple minutes, and I provide them with time to reflect on what they learned.

Look I guess what I’m saying is that you want to define success in such a way that allows every student to feel good about themselves everyday, regardless of past performance.

Why Algebra? – The Basketball Analogy

“I think less of us would drop out if we just knew why the hell we needed this stuff”

That was said by a student who was simplifying rational expressions.  I had a positive relationship with her so the quote was simple honesty and not some veiled attempt at making a teacher feel bad by calling their job pointless.  I knew at that moment I needed to be more purposeful in my attention to the question of ‘Why Algebra?’.

Periodically throughout the year I dedicate a few minutes to tell them why Algebra is important.  I always remind them there are many different reasons, and that no reason by itself will feel sufficient because we are all such different people.  But when we take all the reasons together, the total picture will hopefully be able to answer the question for each student.   I usually start with a basketball analogy because I used to coach basketball.  It’s how I explain that you will need to use algebra in more advanced math.

We learn algebra differently that we learn most things in our life.  For example you generally play basketball first.  And then you decide you want to get better so you practice some rebounding drills.  Then you realize that you need to be able to dribble the ball and you start doing ball handling drills.  Algebra is typically constructed the other way around.  We practice algebra drills without ever playing math – essentially we are practicing dribbling drills without ever playing basketball.  This of course is not always true in algebra class and we are playing math as much as possible in my class – but I’m not trying to spend a lot of time in gray areas to make this point.

With that setup I show the students this video of MIT Instructor Lydia Bourouiba (I begin it at the 1-minute mark) going over a Separable Equations problem in a Differential Equation class.

There are multiple places in this video where she does algebra steps.  Like at the 1:09 mark when she puts all the y-variables on one side of the equation, and the x-variables on the other.  Except she doesn’t show any of her work, she just does it.  In basketball you don’t think about how to dribble, you just dribble.  So here I pause the video and do that step like we would in our class, I multiply both sides by dx, canceling the dx’s on the left.  Then I divide both sides by y^2, canceling the y^2 on the right.  Students are surprised to see that they understand something Lydia is doing, and also wondering why she didn’t show her steps like I did.

I end up pausing the video in several places.

I’m basically showing the class that someone in a multivariable calculus class is using the exact things we practice.  Except that the algebra she uses is not an end unto itself – rather it is another step towards a greater purpose.  She is using algebra in the process of resolving a larger question.

Here’s an exchange I had with a student after I made the points above:

MM – “Similarly, in basketball you practice your cross over dribble because its going to help you in the game.”
Student – “Yeah Mr. Miller, but how are we suppose to remember what we are doing here 10 years from now?”
MM – “Do don’t have to remember it, because you’ll just do it.  When you are playing basketball you don’t remember that first dribbling drill you did 10 years ago.  You just dribble.”

And I shit you not – I saw and heard multiple aha moments around the room.  And then the closing line:

MM – “I know what you are all thinking.  I know if I was you, when I was your age, I would be thinking to myself ‘That’s fine but I still don’t care because I am never going to take that class.’  (pause for laughter and general agreement from the class)  But you never know.  I ended up taking that class”.

That takes a few minutes – and then I begin the days lesson.  Are students instantly motivated?  No.  But at worst the student who honestly thought there was no reason – now knows there is some reason.  Maybe they don’t think that reason applies to them, but they know its there.  And if your students do not embrace the unknown quality of their futures; embrace the fact that they don’t know where these open doors lead – then your job as a motivator is not done yet anyway.